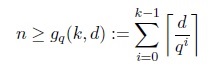
Griesmer Bound for Linear Codes over Finite Fields

Griesmer Bound

An [n,k,d]_q code means a linear code of length n, dimension k and minimum Hamming distance d over the field of q elements GF(q).

n_q(k,d) = the minimum length n for which an [n,k,d]_q code exists.

The Griesmer bound says that an [n,k,d]_q code satisfies

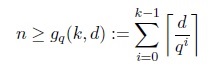
Linear Codes of Dimension k over GF(q) with k = 1 or 2

The Griesmer bound is attained for all d and q for k = 1, 2.

Binary Linear Codes

All values of n₂(k,d) have been determined for k < 9, see
I. Bouyukliev, D.B. Jaffe, Z. Vabrek, The smallest length of eight-dimensional binary linear codes with prescribed minimum distance, IEEE Trans. Inform. Theory 46(4) (2000) 1539--1544.

Linear Codes of Dimension Three over GF(q), 2 < q <= 9

The Griesmer bound is attained for all d except the following, for which n_q(3,d) = g_q(3,d) + 1:

q=3; d=3

q=4; d=7, 8

q=5; d=5, 9, 10, 13, 14, 15

q=7; d=7, 13, 14, 19-21, 25-28, 31-35

q=8; d=13-16, 29-32, 37-40, 43-48

q=9; d=9, 15-18, 25-27, 33-36, 43-45, 49-54, 58-63.

See also Ball's table.

Ternary Linear Codes for k = 4, 5, 6

When k = 4, the Griesmer bound is attained for all d except the following 7 cases:

n₃(4,d) = g₃(4,d) + 1 for d = 3, 7-9, 13-15.

n₃(5,d) table (The Griesmer bound is attained for the missing d in the table.)

n₃(6,d) table

Some 9-divisible ternary linear codes of dimensions 7, 8, 9, 10.

Quaternary Linear Codes for k = 4, 5

When k = 4, the Griesmer bound is attained for all d except the following 30 cases:

n₄(4,d) = g₄(4,d) + 1 for d = 3, 4, 7, 8, 13-16, 23-32, 37-44, 77-80.

n₄(5,d) table (The Griesmer bound is attained for the missing d in the table.)

Linear Codes over GF(5) for k = 4, 5

When k = 4, the Griesmer bound is attained for all d except the following cases:

n₅(4,d) = g₅(4,d) + 1 for d = 4, 5, 9, 10, 12-15, 21-24, 31-50, 61-75, 83-95, 146-150, 163-175.

n₅(4,d) = g₅(4,d) + 2 for d = 25.

n₅(4,d) = g₅(4,d) or g₅(4,d) + 1 for d = 81, 161. <--- only two open cases!

Note (2009):
The nonexistence of [g₅(4,d),4,d]₅ codes for d = 31, 32, 36, 37 was proved by Edel and Landjev.

Note (2015):
The nonexistence of [g₅(4,d),4,d]₅ codes for d = 82, 162 was announced by Rousseva and Landjev at ALCOMA15.

n₅(5,d) table (n₅(5,d) = g₅(5,d) for all d > 1375. )

Linear Codes over GF(7) for k = 4

n₇(4,d) table (n₇(4,d) = g₇(4,d) for all d > 539. )

Linear Codes over GF(8) for k = 4

n₈(4,d) table after On optimal linear codes over F₈

Linear Codes over GF(9) for k = 4

n₉(4,d) table (n₉(4,d) = g₉(4,d) for all d > 1215. )

See Markus Grassl's table for other cases.

If you get a new result improving the tables in this site, please inform it to Tatsuya Maruta.